今天导师在群里分享了一个链接 23 个优秀的机器学习训练公共数据集,看了一下,决定对帕尔默企鹅数据集(Palmer Archipelago (Antarctica) penguin data)做一些分析。
数据集介绍
数据集是在 Kaggle 下载的,包含两个文件:
- penguins_lter.csv:原始数据文件;
- penguins_size.csv:特征约简后的数据文件;
本次分析使用的是简化后的数据集 penguins_size.csv。数据集共 344 个样本,特征信息如下表:
| 特征 | 数据类型 | 说明 |
|---|---|---|
| species | 离散值 | 标签信息,值为 Adelie|Chinstrap|Gentoo 之一 |
| island | 离散值 | 岛屿,值为 Torgersen|Biscoe|Dream 之一 |
| culmen_length_mm | 连续值 | 喙的长度(mm) |
| culmen_depth_mm | 连续值 | 喙的高度(mm) |
| flipper_length_mm | 连续值 | 脚蹼长度(mm) |
| body_mass_g | 连续值 | 体重(克) |
| sex | 离散值 | 性别,值为 MALE| FEMALE 之一 |
数据集包含缺失数据,用 NA 表示特征值缺失,其中第 337 样本的 sex 特征值为“.”,在此也认为是缺失值。
使用 pandas 查看数据集的统计信息:
import pandas as pd
df = pd.read_csv('./dataset/penguins_size.csv', na_values=['NA', '.'])
print(df.describe())
culmen_length_mm culmen_depth_mm flipper_length_mm body_mass_g
count 342.000000 342.000000 342.000000 342.000000
mean 43.921930 17.151170 200.915205 4201.754386
std 5.459584 1.974793 14.061714 801.954536
min 32.100000 13.100000 172.000000 2700.000000
25% 39.225000 15.600000 190.000000 3550.000000
50% 44.450000 17.300000 197.000000 4050.000000
75% 48.500000 18.700000 213.000000 4750.000000
max 59.600000 21.500000 231.000000 6300.000000
显然,统计信息中并不包含离散特征。
缺失数据
对数据集的缺失数据进行一次统计。
# 打印出不完整样本在数据集中的下标
print(df.isna().any(axis=1).where(lambda not_exist: not_exist).dropna().index)
Int64Index([3, 8, 9, 10, 11, 47, 246, 286, 324, 336, 339], dtype='int64')
# 打印出缺失特征值个数统计
print(df.isna().astype(int, False).sum())
species 0
island 0
culmen_length_mm 2
culmen_depth_mm 2
flipper_length_mm 2
body_mass_g 2
sex 11
dtype: int64
使用 missingno 包来查看缺失数据分布:
import missingno as msno
msno.matrix(df)
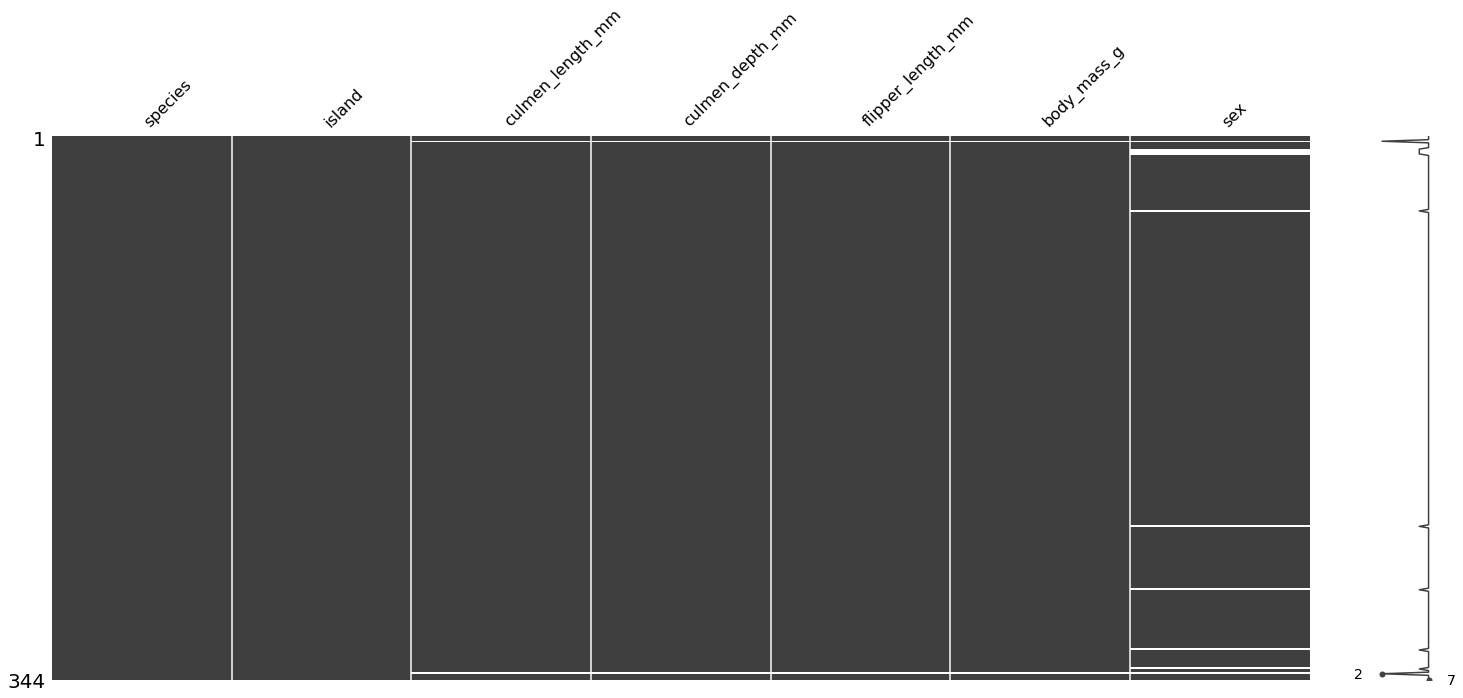
综上,得到以下结论:
- 存在两个样本的 culmen_length_mm、culmen_depth_mm、flipper_length_mm、body_mass_g 和 sex 特征值缺失,编号分别为 3 和 339(以 0 为开始计数);
- 缺失值主要集中在 sex 特征中,共有 11 个样本存在缺失;
预测企鹅性别
预测企鹅性别中,sex 为目标特征,所以先计算连续型特征与目标特征的 Point-biserial 相关系数 $r_{pb} (r_{pb} \in [0, 1])$。
from scipy import stats
# 剔除数据集中不完整样本
df_com = df.drop([3, 8, 9, 10, 11, 47, 246, 286, 324, 336, 339], inplace=False)
# 计算 Point-biserial 相关系数
series_sex = df_com.loc[:,'sex'].copy()
series_sex[series_sex == 'MALE'] = 0
series_sex[series_sex == 'FEMALE'] = 1
print('Point-biserial')
for column in df_com.columns[2:6]:
cor, pvalue = stats.pointbiserialr(series_sex, df_com[column])
print(column, "<=>", 'sex')
print("correlation: ", cor)
print("pvalue: ", pvalue)
print()
Point-biserial
culmen_length_mm <=> sex
correlation: -0.34407778223748564
pvalue: 1.0942555387200282e-10
culmen_depth_mm <=> sex
correlation: -0.37267328821677664
pvalue: 2.0664103457552388e-12
flipper_length_mm <=> sex
correlation: -0.2551688758106061
pvalue: 2.3910970925543724e-06
body_mass_g <=> sex
correlation: -0.4249869909039952
pvalue: 4.897246751596804e-16
$r_{pb}$ 值为负,表示当目标特征 sex 为 0,特征(culmen_length_mm、culmen_depth_mm、flipper_length_mm、body_mass_g)趋向高于 sex 为 1 时对应的值。同时,4 个 p 值均小于 0.05,所以在统计意义上是显著的。
然后计算离散型特征与目标特征的相关性,使用卡方检测进行判断,计算过程可看《卡方检验 - 检验特征对是否相关》。
import numpy as np
from scipy import stats
def chi_significance(x, y):
"""计算离散特征对卡方检验的显著性"""
index = x.unique()
columns = y.unique()
r, c = len(index), len(columns)
count_matrix = np.zeros((r, c))
for i in range(r):
counts = y[x==index[i]].value_counts()
for j in range(c):
if columns[j] in counts.index:
count_matrix[i][j] = counts[columns[j]]
rows_total = np.sum(count_matrix, axis=1)
cols_total = np.sum(count_matrix, axis=0)
total = count_matrix.sum()
estimated_count_matrix = np.zeros((r, c))
for i in range(r):
for j in range(c):
estimated_count_matrix[i][j] = rows_total[i]*cols_total[j]/total
chi = (np.power(count_matrix - estimated_count_matrix, 2) / estimated_count_matrix).sum()
degree = (r - 1) * (c - 1)
return 1 - stats.chi2.cdf(x=chi, df=degree)
for column in ['species', 'island']:
print(column, "<=>", "sex")
print("pvalue: ", chi_significance(df_com[column], df_com['sex']))
species <=> sex
pvalue: 0.9759893689765846
island <=> sex
pvalue: 0.971611229281065
从两对特征的 p 值可知,特征 species、island 与目标特征 sex 的相关性并不显著,所以排除相关。
构建预测模型
从前文的相关性计算可知,目标特征 sex 与特征 species、island 不相关,但是与特征 culmen_length_mm、culmen_depth_mm、flipper_length_mm、body_mass_g 的相关性显著,所以在构建预测模型中不考虑特征 species 和 island。
下面使用支持向量机(Support Vector Machine,SVM)对未知目标特征进行预测,采用 10-Fold 进行交叉验证:
from sklearn.svm import SVC
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
scaler = StandardScaler()
scaler.fit(X)
cv = KFold(n_splits=10, random_state=1, shuffle=True)
clf = make_pipeline(scaler, SVC(
gamma='scale',
C=2.,
kernel='rbf',
random_state=1,
verbose=True,
tol=0.00001
))
scores = cross_val_score(clf, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
print('accuracy: %.3f (%.3f)' % (np.mean(scores), np.std(scores)))
accuracy: 0.904 (0.047)
clf.fit(X, y)
test_X = df.iloc[[8, 9, 10, 11, 47, 246, 286, 324, 336],:][['culmen_length_mm', 'culmen_depth_mm', 'flipper_length_mm', 'body_mass_g']].values
print(clf.predict(scaler.transform(test_X)))
['MALE' 'MALE' 'MALE' 'MALE' 'MALE' 'MALE' 'MALE' 'MALE' 'MALE']
上述完成了以下几件事:
- 将特征 culmen_length_mm、culmen_depth_mm、flipper_length_mm、body_mass_g 作为输入,特征 sex 作为预测值;
- 对输入做标准化处理;
- 采用 10-Fold 交叉验证,输出平均准确率为 0.904,标准差为 0.047;
- 训练模型;
- 预测目标特征;
预测结果如下表:
| 编号 | sex 预测值 |
|---|---|
| 8 | MALE |
| 9 | MALE |
| 10 | MALE |
| 11 | MALE |
| 47 | MALE |
| 246 | MALE |
| 286 | MALE |
| 324 | MALE |
| 336 | MALE |
从预测结果来看,怎么都是 MALE,本能地选择不相信模型结果 -|_|-。
完整代码
import pandas as pd
import missingno as msno
from scipy import stats
import numpy as np
from sklearn.svm import SVC
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
df = pd.read_csv('./dataset/penguins_size.csv', na_values=['NA', '.'])
print(df.describe())
# 打印出不完整样本在数据集中的下标
print(df.isna().any(axis=1).where(lambda not_exist: not_exist).dropna().index)
# 打印出缺失特征值个数统计
print(df.isna().astype(int, False).sum())
msno.matrix(df)
# 剔除数据集中不完整样本
df_com = df.drop([3, 8, 9, 10, 11, 47, 246, 286, 324, 336, 339], inplace=False)
# 计算 Point-biserial 相关系数
series_sex = df_com.loc[:,'sex'].copy()
series_sex[series_sex == 'MALE'] = 0
series_sex[series_sex == 'FEMALE'] = 1
print('Point-biserial')
for column in df_com.columns[2:6]:
cor, pvalue = stats.pointbiserialr(series_sex, df_com[column])
print(column, "<=>", 'sex')
print("correlation: ", cor)
print("pvalue: ", pvalue)
print()
def chi_significance(x, y):
"""计算离散特征对卡方检验的显著性"""
index = x.unique()
columns = y.unique()
r, c = len(index), len(columns)
count_matrix = np.zeros((r, c))
for i in range(r):
counts = y[x==index[i]].value_counts()
for j in range(c):
if columns[j] in counts.index:
count_matrix[i][j] = counts[columns[j]]
rows_total = np.sum(count_matrix, axis=1)
cols_total = np.sum(count_matrix, axis=0)
total = count_matrix.sum()
estimated_count_matrix = np.zeros((r, c))
for i in range(r):
for j in range(c):
estimated_count_matrix[i][j] = rows_total[i]*cols_total[j]/total
chi = (np.power(count_matrix - estimated_count_matrix, 2) / estimated_count_matrix).sum()
degree = (r - 1) * (c - 1)
return 1 - stats.chi2.cdf(x=chi, df=degree)
for column in ['species', 'island']:
print(column, "<=>", "sex")
print("pvalue: ", chi_significance(df_com[column], df_com['sex']))
X, y = df_com[['culmen_length_mm', 'culmen_depth_mm', 'flipper_length_mm', 'body_mass_g']].values, df_com['sex'].values
scaler = StandardScaler()
scaler.fit(X)
cv = KFold(n_splits=10, random_state=1, shuffle=True)
clf = make_pipeline(scaler, SVC(
gamma='scale',
C=2.,
kernel='rbf',
random_state=1,
verbose=True,
tol=0.00001
))
scores = cross_val_score(clf, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
print('accuracy: %.3f (%.3f)' % (np.mean(scores), np.std(scores)))
clf.fit(X, y)
test_X = df.iloc[[8, 9, 10, 11, 47, 246, 286, 324, 336],:][['culmen_length_mm', 'culmen_depth_mm', 'flipper_length_mm', 'body_mass_g']].values
print(clf.predict(scaler.transform(test_X)))
总结
- 离散型特征与连续型特征的相关性可以通过 Point-biserial 相关系数进行衡量;
- 根据卡方检验判断离散型特征间是否相关;
- 预测模型为 SVM,采用 10-Fold 交叉验证的方式,预测出目标特征 sex;
评论