k-means 算法是一种无监督的聚类算法,其优点是逻辑简单、易于实现。
基本原理
质心是指一个簇中样本的均值向量,k-means 中的 means 就是从这里来的。当确定 k 个质心后,需要计算样本与 k 个质心的距离,而样本则归属于距离最近的质心所在的簇。随着算法的迭代,质心的位置会发生变化。质心的变化程度也是算法结束的一个条件,迭代前后质心位置变化通常使用 SSE 来刻画。
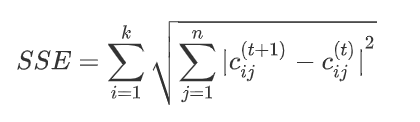
其中 $n$ 是质心的维数,$c^{(t)}_{ij}$ 表示 $t$ 次迭代中第 $i$ 个质心的第 $j$ 维值。
步骤
- 确定 k 值、最大迭代数及误差值;
- 随机选择 k 个样本作为质心;
- 分别计算样本与质心的距离,将样本划分到 k 个簇;
- 重新计算 k 个簇的质心,比较前后质心的误差;
- 若误差小于等于设置的误差值,则算法结束;
- 若误差大于设置的误差值,则执行步骤 5;
- 判断是否达到最大迭代数,若未达到则执行步骤 3,否则算法结束;
问题
选择 k-means 算法做聚类分析时,以下几个问题值得注意:
- 初始质心的选择;
- k 值的确定;
- 距离公式的确定;
k-means 算法容易局部最优,并且算法的结果在很大程度上取决于初始质心的选择,不同的初始质心可能会得到截然不同的聚类结果。同时,在面对未知类别个数的数据集时,如何确定 k 值也是一件麻烦事。通常做法都在小样本集上尝试不同的 k 值,然后比较聚类的结果并将 k 值定为跑得最好结果的那次 k 值。距离公式的选择则是需要依靠领域知识,因为在不同的领域中,样本的相似度的计算方式会有所不同。
完整代码
import numpy as np
import matplotlib.pyplot as plt
def distance(x1, x2):
"""欧式距离"""
return np.sqrt(np.sum(np.power(x1 - x2, 2)))
def sse(centroids1, centroids2):
return np.sum(np.sqrt(np.sum(np.power(centroids1 - centroids2, 2), axis=1)))
def update_centroid(centroids, data):
r, _ = data.shape
cluster_idxs = []
for i in range(len(centroids)):
cluster_idxs.append([])
for i in range(r):
ds = np.array([distance(data[i], centroid) for centroid in centroids])
sorted_idxs = np.argsort(ds)
cluster_idxs[sorted_idxs[0]].append(i)
new_centroids = []
for i, cluster_idx in enumerate(cluster_idxs):
if len(cluster_idx) == 0:
new_centroids.append(centroids[i])
else:
new_centroids.append(np.mean(data[cluster_idx], axis=0))
return np.array(new_centroids)
def initial_centroids(k, data):
r, _ = data.shape
idxs = np.arange(0, r)
np.random.shuffle(idxs)
return data[idxs[:k]]
def cluster(centroids, data):
r, _ = data.shape
cluster_idxs = []
for i in range(len(centroids)):
cluster_idxs.append([])
for i in range(r):
ds = np.array([distance(data[i], centroid) for centroid in centroids])
sorted_idxs = np.argsort(ds)
cluster_idxs[sorted_idxs[0]].append(i)
return cluster_idxs
data = np.random.uniform(5, 10, size=(400, 2))
k = 5
colors = ['#4e9e9d', '#86cc7f', '#506798', '#4f1b63', '#fbe85a']
tol = 1e-6
iteration = 12
plt.figure(figsize=(10, 4))
fig = plt.figure(figsize=(10, 15))
axes = fig.subplots(nrows=3, ncols=2)
centroids = initial_centroids(k, data)
i = 0
while iteration >= 0:
if iteration % 2 == 1:
cluster_idxs = cluster(centroids, data)
for color_idx, cluster_idx in enumerate(cluster_idxs):
fig.axes[i].scatter(data[cluster_idx][:,0], data[cluster_idx][:,1], c=colors[color_idx])
fig.axes[i].scatter(centroids[:,0], centroids[:,1], s=30, marker='*', c='red')
fig.axes[i].set_title('iter %d' % iteration)
i = i + 1
new_centroids = update_centroid(centroids, data)
if sse(new_centroids, centroids) <= tol:
centroids = new_centroids
break
centroids = new_centroids
iteration = iteration - 1
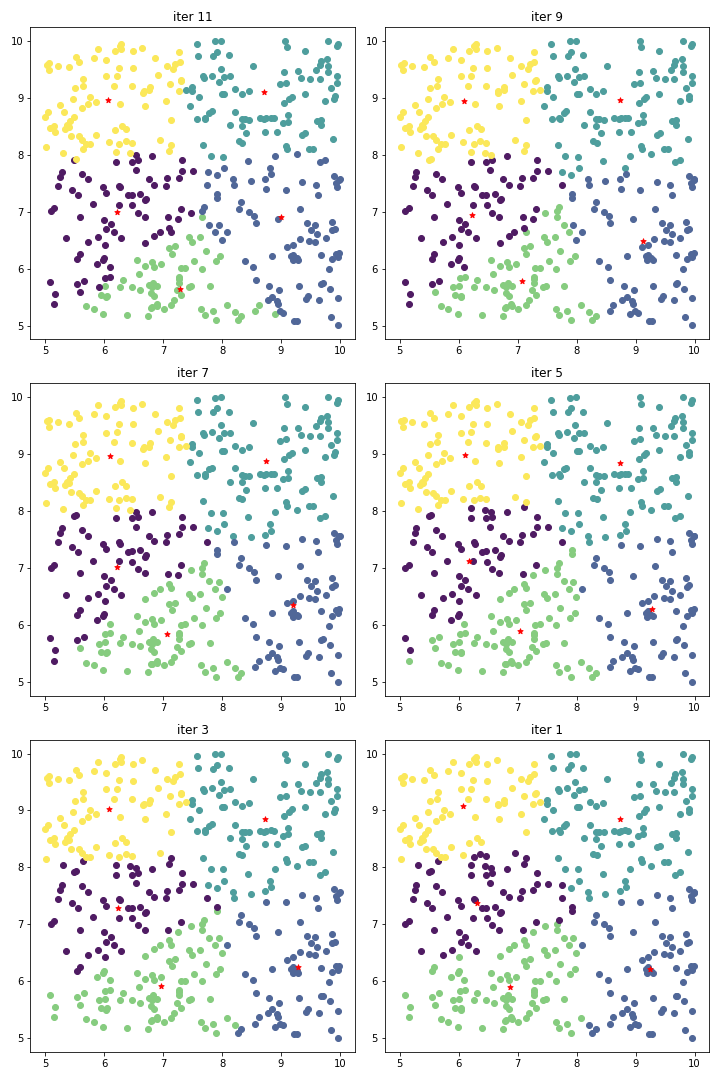
下图是执行得到的一次结果图:
其它
- 帖子讨论了 k-means 和 c-means 是否是相同的概念,得票最多的回答认为是同一概念,所以本文对两者不作区分;
总结
- k-means 算法结束的两个条件;
- 迭代结束;
- 质心位置变化小于误差值;
- Python 实现 k-means 算法;
评论